[ü¬] , [ü®] , [^]
, [ü©]Number of common tangent lines / First result(GC World : Various Problems ,Something strange?)
There are two circles A, B and common tangent lines.
If you move point B, the number of tangent lines will change.
Let's move point B.
How many cases can you make?
You will get following result.
0,2,4
For example, you got figures like these.
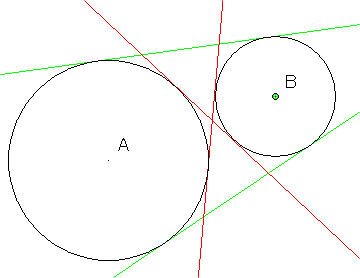
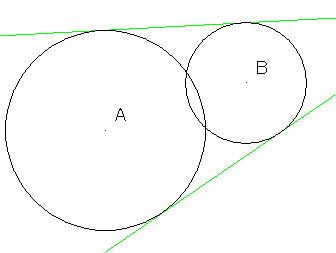
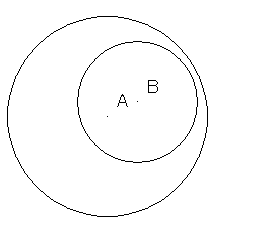
You may not think this is strange. But, there is one strange thing.
There are no cases with an odd number of lines.
Why?
GC/Win


