Sintaxe
Ordem de prioridade
Em princípio, uma expressão é calculada da esquerda para direita.
O interior de um parêntese tem prioridade.
Para outros, a seguinte ordem de prioridade é adotada.
- Função à direita
- Potência
- Multiplicação sem notação
- Função à esquerda
- Multiplicação e divisão
- Adição e subtração
- Operação de comparação e operação lógica
Argumento da função
- Para função à esquerda, o argumento funciona de modo a fazer sentido para operadores aritméticos e lógicos.
Exemplos : sin a cos x2 + 1 = (sin a)(cos x2) + 1
sina(x + 1)2 + 1 = sin (a (x + 1)2) + 1
sina (x + 1)2 + 1 = (sin a)(x + 1)2 + 1
- Se a potência aparece logo depois de uma função trigonométrica, ambas potência e a função são reconhecidas como função.
Exemplo : no caso de "sin2n 2x", "sin2n" é uma função e o argumento é "2x". (O valor é "(sin 2x)2n")
- Os argumentos da função à direita e a potência são a letra na frente delas, o valor e os Parentese.
Exemplo : 2n! = 2 (n!), 2ax2 = 2a (x2)
- Para funções do usuário f, g, h, f1, e f2, o argumento segue do começo de paratese para o fim.
Exemplo : f (cos 2x + 1)2 = (f (cos 2x + 1))2
Se a relação de prioridade não está clara, escreva com parêntese ou separe com espaço.
Exemplos de expressão
Aqui estão alguns exemplos de expressão e suas interpretações.
O sinal de "maior que" (>) na parte da explicação significa relação de prioridade.
| Exemplo |
Interpretação |
Explicação |
| sin2x | sin (2x) |
multiplicção sem sinal > função à esquerda |
| sinx/2 | (sin x) / 2 |
função à esquerda > operação aritmética |
| sinx+2 | (sin x) + 2 |
função à esquerda > operação aritmética |
| sin(x+2) | sin (x + 2) |
prioridade para os parêntese |
| sin(x+1)2 | sin ((x + 1)2) |
potência > função à esquerda |
| sin2x | (sin x)2 |
potência e tratamento especial da função trigonométrica |
| sin2ax | sin (2ax) |
A sequência de caracteres sem separação a torna um argumento. |
| sin2a x | (sin2a) x |
separação com espaço |
| 2x3 | 2 * (x3) |
função à direita > multiplicação sem sinal |
| 1/2x | 1 / (2x) |
multiplicação sem sinal > divisão |
| 1/2 x | (1 / 2) x |
separação com espaço |
| 4+x>1-2x | (4 - x) > (1 - 2x) |
operação aritmética > operação lógica |
Suplemento 1 : Valor Absoluto
O valor absoluto pode ser encontrado usando a notação "[]" ou "abs()", por exemplo "[x + 2]" ou "abs(x + 2)"
Quando GRAPES encontra "[x + 2]", ele interpreta como "abs(x + 2)".
Suplemento 2 : a parte do argumento de uma função
Para a parte do argumento de uma função, temos uso bastante irregular.
Por exemplo,
usamos "f(a+1) x"como "(f (a + 1)) x", mas
"sin(a+1)x" significa "(sin (a + 1)) x" ou "sin ((a + 1) x)" ?
"sinx2"significa "(sin x)2" ou "sin (x2)" ?
"sinax" significa "(sin a) x" ou "sin (ax)" ?
"sina(x+1)" significa "(sin a)(x + 1)" ou "sin (a (x + 1))" ?
"sinxcosy" significa "(sin x)(cos y)" ou "sin (x cos y)" ?
Parece que não existe uma regra explícita para escolher um deles.
GRAPES decide a parte do argumento levando em consideração as seguintes regras, para seguir um consenso na medida do possível.
- Para as funções para as quais os argumentos são usados entre parêntese (f (x), int (x), etc.), o argumento segue do começo do parêntese para o fim.
- Para as funções para as quais os parêntese não são usualmente usados para o argumento (sin x, log x, etc.), considere as seguintes regras :
- separar por espaço, operadores aritméticos, operador lógico, ou operador de comparação.
- não englobar funções.
Tente aplicar estes princípios nos exemplos precedentes.
sin(a+1)x = sin ((a + 1) x)
sinx2 = sin (x2)
sinax = sin (ax)
sina(x+1) = sin (a (x + 1))
sinxcosy = (sin x)(cos y)
Portanto, o princípio geral é:
- usar parêntese para expressões complicadas.
É difícil ? Mesmo que seja, isto permite que você escreva expressões sem ambiguidade.
- A parte do argumento de uma função é mostrada em verde e sublinhada enquanto é inserida na Calculadora.

Suplemento 3 : Σ (Soma de série)
A sintaxe para escrever é Σ (índice, valor inicial, último valor, expressão).
Exemplo : Σ (m, 1, 5, m2) : 12 + 22 + 32 + 42 + 52
- Restrições
- Observe as seguintes restrições.
Se as seguintes restrições não são respeitadas, você não consegue obter resultado correto no cálculo. Em particular, GRAPES não verifica a sintaxe para retrições 2 e 3, por isso você precisa prestar atenção.
- As letras disponíveis para índice são somente a, b, c, d, m, n, p, q, s, t, u, v, θ, e k.
- Uma expressão que contém x não é permitida para os valores inicial ou final do parâmetro.
Exemplo : Σ (k, 1, x, k2) é impossível.
Exemplo : Σ (k, 1, n, k2) é possível.
- Se alguma das funções y1 a y9 aparecer na parte da expressão de Σ, então ela não pode depender do índice da somatória, e os elementos dos objetos elementares não são permitidos.
Exemplo : se y1 = kx, Σ (k, 1, 5, y1) é impossível.
Exemplo : se f (x) = kx, Σ (k, 1, 5, f (x)) é possível.
Exemplo : se y1 = x^2, Σ (k, 1, 5, k + y1) é possível.
- Você não pode englobar Σ numa expressão.
Exemplo : y1 = Σ (n, 1, 10, Σ (k, 2, n, k2)) é impossível.
Exemplo : Se f (x) = Σ (k, 2, n, k2), y1 = Σ (n, 1, 10, f (x)) é possível.
Suplemento 4 : 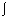 (integral definida)
(integral definida)
- Escreva
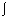 (variável, inf, sup, expressão), ondeos limites da integral são inf = inferior e sup = superior, expressão = integrando.
(variável, inf, sup, expressão), ondeos limites da integral são inf = inferior e sup = superior, expressão = integrando.
- Para calcular integral definida, GRAPES aplica o Método de Simpson. Você pode configurar o número de partições na janela da [Integral Definida].
- Restrições
- Observe as seguintes restrições.
Se as seguintes restrições não forem respeitadas, você não consegue obter resultado correto no cálculo. Em particular, GRAPES não verifica a sintaxe para as restrições 2 e 3, assim você precisa prestar atenção.
- Os parâmetros e as letras x e y podem ser usados como variável da integração.
Mas, x e y não estão disponíveis como variável da integração num ponto ou nas curvas.
- Uma expressão que contém x não é permitida para os limites inferior e superior do intervalo de integração.
- Na expressão, as funções de y1 a y9, que contenham a variável de integração, e os objetos elementares não estão disponíveis.
- O integrando = expressão não pode conter a própria integral..


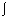 (integral definida)
(integral definida)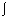 (variável, inf, sup, expressão), ondeos limites da integral são inf = inferior e sup = superior, expressão = integrando.
(variável, inf, sup, expressão), ondeos limites da integral são inf = inferior e sup = superior, expressão = integrando.