Syntax
Order of priority
An expression is in principle evaluated from left to right.
The interior of a parenthesis has a priority.
For others, the following order of priority has been adopted.
- Right function
- Power
- Multiplication without notation
- Left function
- Multiplication and division
- Addition and subtraction
- Comparative operation and logic operation
Argument of function
- For the left function, the argument is till one of arithmetic operators, logical operators, comparative operators, space or left function appears.
Examples : sin a cos x2 + 1 = (sin a)(cos x2) + 1
sina(x + 1)2 + 1 = sin (a (x + 1)2) + 1
sina (x + 1)2 + 1 = (sin a)(x + 1)2 + 1
- If the power is just after the trigonometric function, both the power and the trigonometric function are recognized as a function.
Example : in the case of "sin2n 2x", "sin2n" is a function and the argument is "2x". (The value is "(sin 2x)2n")
- The arguments of the right function and the power are just the letter in front of them, the value, and the parentheses.
Example : 2n! = 2 (n!), 2ax2 = 2a (x2)
- For the user functions f, g, h, f1, and f2, the argument is from the begining of paratheses to the end.
Example : f (cos 2x + 1)2 = (f (cos 2x + 1))2
If the relation of priority is not clear, write with parentheses or separate by space.
Examples of expression
Here is some examples of expression and their interpretations.
The greater-than sign (>) in the explanation part means the relation of priority.
| Example |
Interpretation |
Explanation |
| sin2x | sin (2x) | multiplication without sign > left function |
| sinx/2 | (sin x) / 2 | left function > arithmetic operation |
| sinx+2 | (sin x) + 2 | left function > arithmetic operation |
| sin(x+2) | sin (x + 2) | priority for the parentheses |
| sin(x+1)2 | sin ((x + 1)2) | power > left function |
| sin2x | (sin x)2 | power and exceptional treatment of trigonometric function |
| sin2ax | sin (2ax) | The character sequence without separation becomes an argument. |
| sin2a x | (sin2a) x | separation by space |
| 2x3 | 2 * (x3) | right function > multiplication without sign |
| 1/2x | 1 / (2x) | multiplication without sign > division |
| 1/2 x | (1 / 2) x | separation by space |
| 4+x>1-2x | (4 - x) > (1 - 2x) | arithmetic operation > logical operation |
Supplement 1 : Absolute value
The absolute value can be found by using the notation "[]" or "abs()", for example "[x + 2]" or "abs(x + 2)"
When GRAPES encounters "[x + 2]", it will interprete it as "abs(x + 2)".
Supplement 2 : the argument part of function
For the argument part of function, we have the very irregular usage.
For example,
We use "f(a+1) x" as "(f (a + 1)) x", but
"sin(a+1)x" means "(sin (a + 1)) x" or "sin ((a + 1) x)" ?
"sinx2" means "(sin x)2" or "sin (x2)" ?
"sinax" means "(sin a) x" or "sin (ax)" ?
"sina(x+1)" means "(sin a)(x + 1)" or "sin (a (x + 1))" ?
"sinxcosy" means "(sin x)(cos y)" or "sin (x cos y)" ?
It looks as if there is no explicit rule for which one to choose.
GRAPES decides the argument part by taking into account the following rules,
in order to follow common sense as much as possible.
- For the functions for which the parentheses of argument are usually used (f (x), int (x), etc.), the argument is from the beginning of parentheses to the end.
- For the functions for which the parentheses of argument are not usually used (sin x, log x, etc.), take into account the following rules :
- separate by space, arithmetic operators, logical operator, or comparative operator.
- do not nest the functions.
Try to apply these principles to the precedent examples.
sin(a+1)x = sin ((a + 1) x)
sinx2 = sin (x2)
sinax = sin (ax)
sina(x+1) = sin (a (x + 1))
sinxcosy = (sin x)(cos y)
Therefore, the general principle is
- to use parentheses for the complicated expression.
Is it hard ? Even if it is, it will enable you to write unambiguous expression.
- The argument part of function is shown with green underbars while inputting on the calculator.

Supplement 3 : Σ (Sum of series)
The syntax is write like Σ (index, initial value, last value, expression).
Example : Σ (m, 1, 5, m2) : 12 + 22 + 32 + 42 + 52
- Restrictions
- Note the following restrictions.
If the following restrictions are not respected, you cannot get the correct calculation results. In particular, GRAPES does not verify the syntax for the 2 and 3 restrictions, so, you have to pay attention by yourself.
- The available letters for index are only a, b, c, d, m, n, p, q, s, t, u, v, θ, and k.
- An expression containing x is not permitted for the initial or the final values of the parameter.
Example : Σ (k, 1, x, k2) is impossible.
Example : Σ (k, 1, n, k2) is possible.
- If any of the function y1 to y9 appears in the expression part of Σ, then it cannot depend on the index of summation, and the elements of elementary objects are not permitted.
Example : if y1 = kx, Σ (k, 1, 5, y1) is impossible.
Example : if f (x) = kx, Σ (k, 1, 5, f (x)) is possible.
Example : if y1 = x^2, Σ (k, 1, 5, k + y1) is possible.
- You cannot nest Σ in an expression.
Example : y1 = Σ (n, 1, 10, Σ (k, 2, n, k2)) is impossible.
Example : If f (x) = Σ (k, 2, n, k2), y1 = Σ (n, 1, 10, f (x)) is possible.
Supplement 4 : 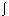 (definite integral)
(definite integral)
- Write
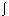 (variable, inf, sup, expression), where inf = lower and sup = upper limit of the integral, expression = the integrand.
(variable, inf, sup, expression), where inf = lower and sup = upper limit of the integral, expression = the integrand.
- To calculate definite integration, GRAPES applies Simpson Method. You can configure the number of partitions in the [Definite integral window].
- Restrictions
- Note the following restrictions.
If the following restrictions are not respected, you cannot get the correct calculation results. In particular, GRAPES does not verify the syntax for the 2 and 3 restrictions, so, you have to pay attention by yourself.
- The parameters and the letters x and y can be used as an integration variable.
But, x and y are not available as an integration variable in the point or the curves.
- An expression containing x is not permitted for the infimum (lower bound) and the supremum (upper bound).
- In the expression, the functions from y1 to y9, containing the integration variable, and the elementary objects are not available.
- The integrand = expression cannot contain the integral itself.


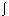 (definite integral)
(definite integral)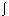 (variable, inf, sup, expression), where inf = lower and sup = upper limit of the integral, expression = the integrand.
(variable, inf, sup, expression), where inf = lower and sup = upper limit of the integral, expression = the integrand.