Ingredientes de expressões
Função à esquerda (i.e. f(x) em vez de (x)f)
- sin, cos, tan, Asin, Acos, Atan : função trigonométrica, e suas inversas (letra A denota função inversa)
Para selecionar se usa grau ou radiano, configure em [Opção | Opções de Função] da barra de Menu.
- exp : exponencial (ex)
- log (base, antilogaritmo) : logaritmo com base (por exemplo, "log (2, 8) = 3"). Se a base estiver omitida, será Logaritmo Natural ou Logaritmo Comum, i.e. log na base e ou 10.
Você pode selecionar o logaritmo sem base (Natural or Common) com "Logaritmos" em [Opção | Opções de Função] da barra de Menu.
O padrão é Logaritmo Natural.
- Em : Logaritmo Natural (isto está disponível, apesar de não haver botão correspondente na calculadora)
- Sqrt, Cbrt : raíz quadrada, raíz cúbica
- int, round : parte inteira (equivalente à notação de Gauss), arredondamento
- frc : frc (x) = x - int (x)
- mod : resto
- abs, sign : valor absoluto, sinal
O valor absoluto de um número pode também ser dado por "[" e "]" (exemplo : [x])
sign (número positivo) = 1, sign (número negativo) = -1, sign (0) = 0
- nCr( , ) : coeficiente binomial, também dado por (nr)
Se o argumento for um número real, ele será calculado após arredondamento.
- rnd (x) : o domínio de rnd (x) é contituído de números reais >= 0.5
Para calcular rnd (x), o primeiro x é arredondado, digamos [x].
Se [x] = 1 então rnd (x) é um número real randômico entre 0 e 1.
Se [x] > 1 então rnd (x) é um dos inteiros 0, 1, 2, ..., [x] - 1 escolhido randômicamente.
- max (x1, x2, ..., xn), min (x1, x2, ..., xn) : máximo, mínimo
O número de argumentos deve ser mais que 1 e menos que 20, e ser escrito separando-os com vírgula.
Entre os argumentos válidos, o máximo ou o mínimo será dado.
Exemplo : max (-2x, 2, x+1)
- f, g, h, f1, f2 : funções do usuário
- f', g', h', f1', f2' : derivadas das funções do usuário
- f'', g'', h'', f1'', f2'' : derivadas segundas das funções do usuário
- F, G, H, F1, F2 : integrais indefinidas das funções do usuário, somente para polinomiais de grau menor ou igual a 9. Em outros casos o valor da integral não será dado.
- F(x) : integração de f (x) com sup x e inf 0.
- det (x1, y1, x2, y2) Nota : determinante x1y2 - x2y1
- área (x) : área (0) é um mínimo de x, área (1) é um mínimo de y, área (2) é um máximo de x, e área (3) é um máximo de y.
- Passo (parâmetro) : fornece o valor do incremento do parâmetro indicado e mostrado área de parâmetro.
Esta função é principalmente usada com script.
Função que tem expressão como argumento
- cof (ordem, expressão) : fornece o coeficiente de uma dada potência de x numa polinomial de grau menor que 7.
Exemplo : cof (2, 4x3 + 5x2 - 6x + 1) = 5
A ordem precisa ser um inteiro.
- Σ : Soma de série (Exemplo : Σ (m, 1, 5, m2) = 12 + 22 + 32 + 42 + 52)
Para mais detalhes, veja Sintaxe.
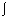 : Igr : integral definida
: Igr : integral definida 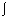 (variável, inf, sup, expressão)
(variável, inf, sup, expressão)
(Exemplo : 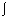 (t, 1, 5, t2))
(t, 1, 5, t2))
Para mais detalhes, veja Sintaxe.
Função que tem vetor como valor
- (x1, y1) : vetor cuja componente x é x1 e a componente y é y1
- mid (P1, P2) : ponto médio entre dois pontos
- mid (P1, P2, m, n) : ponto que divide o segmento P1P2 na razão m : n
- Esta função não é necessária se usar a fórmula para dividir um segmento.
Esta função é considerada para ser usada em aulas de geometria na primeira série do ensino médio. Quase todas as funções a seguir são usadas num curso de geometria.
- rot (P) : rotaciona o vetor P em 90°.
- rot (P, t) : rotaciona o vetor P em t graus.
A unidade do ângulo de rotação é medida em radiano, por padrão. Para mudar para medida em grau, selecione [Grau] em [Unidade de Ângulo] em [Opção | Opções de Função].
- rot (P, A, t) : rotaciona P em t graus em torno do ponto A
- Intr (A1, A2, B1, B2) : interseção da reta A1A2 com a reta B1B2
- perp (P, A, B) : pé da perpendicular de P à reta AB
- Ccentr (P1, P2, P3) : circuncêntro do triângulo P1P2P3
- Icentr (P1, P2, P3) : incentro do triângulo P1P2P3
- Hcentr (P1, P2, P3) : ortocentro do triângulo P1P2P3
- Gcentr (P1, P2, ..., Pn) : baricentro do polígono com n vértices P1, P2, ..., Pn
Funções reais com vetores como argumento
- P.x : componente x do vetor P, P.y : componente y do vetor P
- |P| : comprimento do vetor (para inserir, use "[P]". É igual ao valor absoluto)
- Exemplo : distância entre o ponto P e (2, 3) : [P - (2, 3)]
- [PQ] significa comprimento do segmento PQ.
- dis (P1, P2) : distância entre dois pontos
- det (P1, P2) : valor do determinante
- O determinante de matriz 2*2 composta de of a, b, c, e d é "det ((a, b), (c, d))" ou "det (a, b, c, d)".
- path (x, P1, P2, ..., Pn) : polinomial de grau (n - 1) que passa por n pontos
- arg (P) : Ângulo entre o vetor P e eixo x.
- O intervalo do ângulo, "de 0 a 2π" ou "de -π a π", pode ser selecionado em Opções de Função.
- arg (P, Q, R) : ângulo PQR.onde Q denota o vértice.
- Se Q for origemn O, arg (P, O, R) pode também ser escrito como arg (P, Q).
- O formato onde a vírgula está omitida, como "arg (PQR)", não está disponível.
- Irad (P1, P2, P3) : raio do círculo inscrito
- Crad (P1, P2, P3) : raio do círculo circunscrito
Função do usuário e vetor
- Uma função do usuário pode ter vetor como valor.
- Exemplo : f (x) = xP + (1 - x) Q
- Uma função do usuário de duas variáveis pode ter vetor como argumento..
- f (2, 3) significa calcular o valor de f para x = 2 e y = 3.
f ((2, 3)) significa substituição do vetor (2, 3) como argumento de f, mas o resultado é o mesmo.
- Para outras funções, é estritamente diferente "colocar dois argumentos" e "colocar vetor como argumento", com exeção de arg.
Por exemplo, log (2, 8) = 3 , mas log ((2, 8)) não está definido e portanto será rejeitado.
rot (2, 3) é também rejeitado, mas rot ((2, 3)) = (-3, 2).
- Exemplo 1 : para f (x, y) = x + y , se P = (2, 3), f (P) = 2 + 3 = 5
- Exemplo 2 : para f (x, y) = xA + yB, se P = (2,3), f (P) = 2A + 3B
Função à direita (i.e. (x)f, onde o símbolo da função aparece à direita do argumento)
- ! : fatorial
Se o argumento for um número real, será calculado após arredondamento.
- ° : transforma grau para radiano (não funciona quando grau é configurado para substituir radiano)
- .x : componente x do vetor
Exemplo : (2, 3).x = 2
- .y : componente y do vetor
- .r : raio do círculo (objeto elementar)
Função sem argumento
- π, e : pi e base do logaritmo natural
- y1 ... y20 : valores de funções
estes não estão disponíveis quando define uma função do usuário ou componentes de figuras.
- P, Q, etc. : coordenadas das figuras
- r, θ (somente quando escritos na expressão de uma relação) : r = len (x, y), θ = arg (x, y)
Operador
- +, -, ×, / : quatro operações aritméticas
Elas são válidas também para as operações com vetor:
adição, subtração, e produto por escalar.
- · : produto intern de vetores
- ^ : potência por um número real
Se estiver depois de uma função trigonométrica GRAPES interpreta como uma potência do valor da função.
(Exemplo : sin^n x = (sin x)^n)
- >, >=, <, <=, <>, = : operadores de comparação
Eles tomam valor "1" se for "verdadeira" e retorna "erro" se for "falsa".
(Exemplo : para y = (x > 2) sin x, GRAPES desenha o gráfico de y = sin x apenas para x > 2)
- e, ou, não : operadores lógicos
Eles tomam valor "1" se for "verdadeira" e retorna "erro" se for "falsa".
Parêntese ( )
Há três significados para parêntese.
- Os parêntese dão prioridade à expressão a ser calculada.
- Os parêntese com dois números reais significa um vetor.
Exemplo: (2, 3)
- Ele representa também o domínio de uma função.
Exceções : função trigonométrica, funções trigonométricas inversas, exp, logaritmo, raíz quadrada, raíz cúbica.
Parâmetro
- a, b, c, d, k, m, n, p, q, s, t, u, v, θ
θ náo está disponível como parâmetro numa relação e funções do usuário, porque ele é tratado como uma função que expressa um argumento.
Para usar θ como um parâmetro nestas funções, configure em Opções de Gráfico.
Variáveis
- x, y
Em objetos elementares, x e y significam seus componentes.
- r, θ
Nas funções do usuário e nas relações, r = Sqrt (x2 + y2) , θ = arg (x, y).
- X
isto significa um ponto (x, y). (usamos nas funções do usuário ou numa relação)
Vetor
- X : ponto (x, y)
- O : origem (0, 0)
- P, Q, R, S, T, A, B, C, D, E, F, G, H, I, J, K, L, M, N : objetos elementares e pontos sobre curvas
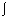 : Igr : integral definida
: Igr : integral definida 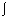 (variável, inf, sup, expressão)
(variável, inf, sup, expressão) 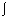 (t, 1, 5, t2))
(t, 1, 5, t2))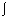 : Igr : integral definida
: Igr : integral definida 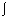 (variável, inf, sup, expressão)
(variável, inf, sup, expressão) 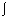 (t, 1, 5, t2))
(t, 1, 5, t2))