Vetor e Ponto

Preliminares

• Não há distinção entre um ponto e um vetor: todos pontos podem ser consideradaos como vetores posição.
• GRAPES trata qualquer par ordenado de números reais como um vetor.
  Exemplo: (2, 3)
• Se dois objetos elementares são escritos justapostos, GRAPES trata como um vetor deslocamento.
  Exemplo: se escrever PQ numa expressão, isto significa um vetor PQ. Ele é o mesmo que Q - P.
• Você pode inserir uma expressão vetorial diretamente sem decompô-lo em componentes.
  • Exemplo: o ponto médio de B e C pode ser inserido como (B + C) / 2.
• Operação Vetorial
  • Adição, subtração, produto interno, e produto por escalar são disponíveis.
• Função que tem vetores como seus valores (As seguintes são as principais funções)
  • A função que fornece o ponto médio ou ponto que divide um segmento segundo razão a : b.
  • Função que define uma rotação.
  • Função que fornece a interseção de duas retas.
  • Função que fornece o circuncentro.
• Função real que tem vetor como argumento (As seguintes são as principais funções)
  • |P|: o comprimento do vetor (inserir "[P]", i.e. é o mesmo que valor absoluto).
  • O valor do determinante.
  • Função que dá a medida de um ângulo.
• Função do usuário e vetor
  • Função do usuário pode ter vetor como valor da função..
  • Função do usuário pode ter vetor como argumento.
• Funções reais com variãvel vetorial podem ser deiferenciadas, integradas de a a b, somado (sigma) segundo um número finito de vetores. A integral indefinida de uma função assim não está definida.

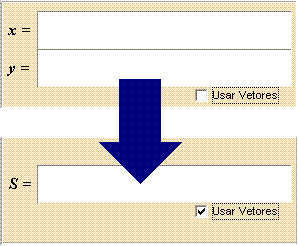
Como inserir objetos elementares e curvas com vetores ?

• Assinale a caixa [Usar Vetores] na janela de Propriedades depois de selecionar o tipo da figura.
• Insira a expressção com vetores.
  • Exemplo 1: (P + Q) / 2 : o ponto médio entre dois pontos.
  • Exemplo 2: P + (1, 2) : a translação de P pelo vetor (1, 2).

A relação entre vetores e pontos (objetos elementares e curvas)

• Ponto e vetor são equivalentes. Não há diferenças.
  Exemplo : (2P + 3Q) / 5 significa um ponto dado pela divisão do segmento PQ segundo a razão 3 : 2 .
• x -coordenada do ponto P é P.x, y- coordenada é P.y.
  Exemplo : Seja P = (2, 3), e neste caso P.x = 2, P.y = 3.
  • o raio do círculo: o raio do círculo P é P.r.
• Se dois objetos elementares são escritos justapostos, isto é reconhecido como sendo um vetor deslocamento.
  Exemplo: a expressão PQ significa vetor PQ. A seta será mostrada na Calculadora.
  • É claro que o vetor PQ é isual a Q - P.
  • [PQ] significa comprimento do segmento PQ.
• Você pode inserir coordenadas x e y , sem precisar decompor um vetor em suas componentes.
  • Assinale a caixa [Usar Vetores] na janela de Propriedades após selecionar o tipo de figura.
  • Exemplo: quando um objeto elementar como um ponto A é o ponto médio entre B e C, insira (B + C) / 2.

Criar vetores e extrair componentes

• Sempre que dois números ou expressões são inseridos entre parêntese com ',' entre os mesmos, isto será interpretado como um vetor com componentes x e y.
• Exemplo: (2, 3) ; (t - sin t, 1 - cos t)
  • Reciprocamente, dado um vetor (x, y), a função '.x' extrai a componente x (observe que o símbolo de função é escrito no lado direito da componente). Por exemplo,
    • .x : componente x do vetor (2, 3) é (2, 3).x = 2
    • .y : componente y do vetor (2, 3) é (2, 3).y = 3

  ---